Pengertian dan Penjelasan Besaran Vektor - Perhatikan dua anak yang mendorong meja pada gambar di di bawah ini!. Apakah dua anak tersebut dapat mempermudah dalam mendorong meja? Tentu kalian sudah mengerti bahwa arah gaya dorong sangat menentukan, keduanya memiliki arah berlawanan sehingga akan mempersulit. Contoh lain seperti perahu yang menyeberangi sungai yang deras arusnya.
Penyelesaian masalah-masalah ini perlu keterlibatan suatu besaran yaitu besaran vektor. Besaran inilah yang dapat kalian pelajari pada bab ini, sehingga setelah belajar kalian diharapkan dapat:
Anak panah dapat memberikan dua sifat yang dimiliki oleh vektor. Panjang anak panah menggambarkan nilai vektor sedangkan arah anak panah menggambarkan arah vektornya. Perhatikan contohnya pada Gambar 2.2! Gaya F1 besarnya 1 N arahnya ke kanan. Dengan acuan F1 dapat ditentukan F2, yaitu besarnya 3 N arahnya ke kanan, karena panjang F2 = 3 kali F1 dan arahnya sama.
Jika diketahui dua komponen vektornya maka vektor yang diproyeksikan itu juga dapat ditentukan yaitu memenuhi dalil Pythagoras. Persamaannya sebagai berikut.
Apakah kalian bisa memahami penjelasan di atas, persamaan 2.1 dan persamaan 2.2? Untuk memahami penggunaan persamaan 2.1 dapat kalian cermati penjelasan tambahan berikut.
Perhatikan contoh di bawah ini, dan diskusikan dengan teman-teman di Sekolah.!
Demikian sekilas informasi mengenai Pengertian dan Penjelasan Besaran Vektor dalam Berbagai Soal Serta Pembahasannya. Semoga bermanfaat, salam.
 |
| Gambar Anak mendorong meja |
- Memahami definisi besaran vektor,
- Menguraikan sebuah vektor menjadi dua komponen saling tegak lurus dan sebidang,
- Menjumlahkan dua vektor sejajar dan vektor tegak lurus,
- Menjumlahkan dua vektor atau lebih dengan metode jajaran genjang,
- Menjumlahkan dua vektor atau lebih dengan metode poligon,
- Menjumlahkan dua vektor atau lebih dengan metode analitis,
Aba-aba ini dapat berarti berilah kecepatan yang besarnya tetap dengan arah ke belakang. Contoh yang lain adalah mendorong benda dengan gaya tertentu. Misalnya ada meja yang berada di tengah aula. Kemudian Andi diminta bapak guru untuk mendorong meja dengan gaya tertentu.
Dapatkah Andi melakukannya dengan benar? Bisa jadi ada kesalahan. Supaya Andi dapat mendorong dengan benar maka sebaiknya harus ditunjukkan arahnya, misalnya dorong ke kanan dan meja dapat berpindah sesuai keinginan bapak guru. Beberapa contoh besaran di atas selalu melibatkan nilai besaran itu dan butuh arah yang tepat.
Besaran yang memiliki sifat seperti inilah yang disebut besaran vektor.
1. Penjelasan Besaran Skalar dan Vektor
Di dalam ilmu dikenal banyak sekali besa ran. Masih ingat ada berapakah jenis besaran menurut satuannya? Tentu masih karena baru saja kalian pelajari bab pertama buku ini, yaitu ada dua : besaran pokok dan besaran turunan. Besaran juga dapat kalian bagi berdasarkan nilai dan arahnya. Berdasarkan nilai dan arahnya seperti contoh anak mendorong meja di atas, besaran dapat dikelompokkan menjadi dua, yaitu besaran vektor dan besaran skalar.
Besaran vektor adalah besaran yang memiliki nilai dan arah. Besaran ini selain dipengaruhi nilainya juga akan dipengaruhi oleh arahnya. Contoh besaran ini adalah perpindahan. Ali berpindah 2 meter. Pernyataan ini kurang lengkap, yang lebih lengkap adalah Ali berpindah 2 meter ke kanan. Nilai perpindahannya 2 meter dan arahnya ke kanan.
Contoh besaran vektor yang lain adalah kecepatan, gaya dan momentum. Besaran skalar adalah besaran yang memiliki nilai saja. Contoh besaran skalar adalah massa. Perlukah kalian menimbang massa benda untuk mencari arah massa itu? Tentu tidak. Menimbang massa hanya dihasilkan nilai saja misalnya massa kalian 60 kg, berarti nilai massa itu 60 kg dan tidak memiliki arah.
Contoh besaran skalar yang lain adalah jarak, waktu, volume dan energi.
2. Penggambaran Vektor
Untuk menulis suatu besaran vektor dapat langsung menyebutkan nilai dan arahnya, misalnya gaya F = 20 N ke kanan, kecepatannya v = 100 km/jam ke utara dan berpindah sejauh 5 m ke barat. Tetapi untuk mempermudah pemahaman dan analisa, besaran vektor dapat diwakili dengan gambar yang berlaku secara universal yaitu gambar anak panah.
3. Penguraian Vektor
Coba kalian perhatikan sebuah balok bermassa m yang ditarik gaya F yang membentuk sudut α terhadap horisontal seperti pada Gambar 2.4(a) di bawah ini.
Jika lantainya licin maka kemanakah balok akan bergerak? Tentu kalian langsung dapat memprediksikannya, yaitu ke kanan. Tetapi dapat ditanya kembali, mengapa dapat bergerak seperti itu? Gaya F merupakan besaran vektor. Vektor F ini dapat diproyeksikan ke arah horisontal FX dan ke arah vertikal FY seperti pada Gambar 2.4(b).
Jika FY lebih kecil dibanding berat benda dan lantai licin maka balok akan bergerak searah FX yaitu arah horisontal ke kanan. Contoh kejadian di atas ternyata berlaku umum untuk vektor.
Setiap vektor dapat diuraikan menjadi dua komponen yang saling tegak lurus. Komponen-komponen penguraian vektor ini disebut juga proyeksi vektor. Besar komponen atau proyeksi vektor ini memenuhi perbandingan trigonometri seperti persamaan berikut.
Perhatikan persamaan di bawah ini:
 |
| Persamaan penguraian vektor |
 |
| Persamaan penguraian vektor |
 |
| Penjelasan penguraian vektor |
Sebuah perahu bergerak dengan kecepatan v = 0,5 m/s dengan arah seperti Gambar 2.5(a). Jika airnya relatif tidak bergerak maka tentukan proyeksi kecepatan perahu pada arah utara dan timur!
Penyelesaian Proyeksi kecepatan perahu dapat dilihat seperti pada Gambar 2.5(b). Sesuai persamaan 2.1, maka besarnya proyeksi kecepatan itu dapat memenuhi perhitungan berikut.
Jawab:
Secara sederhana, berikut pola gambar dari soal di atas.
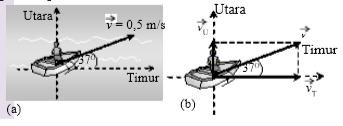 |
| Penjelasan gambar soal vektor |
Berikut ini adalah jawabnnya:
Demikian sekilas informasi mengenai Pengertian dan Penjelasan Besaran Vektor dalam Berbagai Soal Serta Pembahasannya. Semoga bermanfaat, salam.


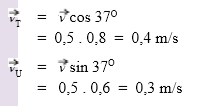
0 Response to "Pengertian dan Penjelasan Besaran Vektor dalam Berbagai Soal Serta Pembahasannya"
Silakan masukkan komentar Sobat di bawah ini. Komentar di luar topik dan menanamkan link hidup atau mati tidak akan dimunculkan. Terimakasih. Salam